Theorem prover, symbolic execution and practical reverse-engineering

Security Day 2015 - Lille 1 University - France

16th of January 2015

Axel '@0vercl0k' Souchet

Table of Contents

Introduction

Who is this guy?

  • Young security researcher @ MSRC by day

  • CS graduate since June 2013, security enthusiast since forever

  • Love all kind of security and low level subjects: code obfuscation, system programming, software vulnerability exploitation, reverse-engineering, etc.

  • Where I like to blog: doar-e.github.io/

  • Where I post codes: github.com/0vercl0k

  • Where I tweet: twitter.com/0vercl0k

What are we going to talk about?

  • Microsoft's Z3 theorem prover..

  • ..and its Python bindings

  • Symbolic execution

  • Assemblies: Intel x86 & MIPS

  • Long story short: how Z3 & symbolic execution can help you tackle reverse-engineering / security problems in an elegant way

What we won't talk about?

  • Won't bother you with theoretical stuff ;-)

  • Won't talk about how theorem provers do their magic

Theorem provers

What it is in a few words

  • “A collection of little engines of proof” Leonardo De Moura, 2009

  • I like to see it as a "software black-box oracle"

  • You give it an equation, it gives you back an answer

    • If satisfiable: you get a model

  • Easy right?

Why on earth do you need that?

Z3 101

Presentation

Installation on Windows for Python

  • Nice and neat Windows installers are here

  • Run that in a Python shell to make sure the installation went fine 

    •                                 
import z3

Z3py Hello-World

                            from z3 import *
a, b = BitVecs('a b', 32)
s = Solver()
s.add((a + b) == 1337)
if s.check() == sat:
    print s.model()
else:
    print 'Unsat'

Z3py Hello-World: Explanations I

  • BitVecs are basically arrays of 0 & 1's

  • It is the type the closest from what your CPU handles

  • A BitVec8 is basically the equivalent of an unsigned char variable in C

  • A solver instance holds a set of constraints you want to apply

  • Obviously, you can apply constraints only on Z3 variables: not on normal Python variables

Z3py Hello-World: Explanations II

  • BitVecs are not the only type available, you can also use: Ints, Bools, Arrays, etc.

    • Note that Z3 integers are integers like in math: they are infinite ; as opposed to BitVecs

  • Why :-)?

    • BitVecs do wrap, like CPU registers or C integers

Z3py Hello-World: Explanations III

  • Important detail: Z3 data-types don't hold any signess information

  • Operators do

  • You have operators for signed & unsigned operations:

    • Signed operators: <, <=, >, >=, /, %and, >>

    • Unsigned operators: ULT, ULE, UGT, UGE, UDiv, URemand, LShR

Z3py tips: solve & Solver

  • Maybe the most important function: this is the function that will answer your questions

  • If solvable, it gives you a model (even if several exist) which is basically concrete values for your symbolic variables

Z3py tips: Solver & backtracking points

  • You can create backtracking points by using push and pop

  • It basically saves the constraints you have set in the solver: it's a checkpoint

  • As the name suggests, it's particularly useful when using backtracking algorithms

Z3py tips: simplify

  • This function is something really important: as the name suggests it can simplify Z3 expressions

  • Keep in mind it's not magic though: the returned expression does not have to be the most simplified expression (cf Breaking Kryptonite's Obfuscation)

  • A lot of options can be enabled / disabled to help simplify to do a better job at simplifying ; call help_simplify()

Z3py tips: ZeroExt, SignExt

  • Two useful functions when you deal with BitVecs

  • As their names suggest, they basically zero or sign extend a BitVec

  • Use case: zero extend a 32 bits BitVec into a 64 bits BitVec

Z3py tips: Extract, Concat

  • Another couple of useful functions:

    • Extract: Extract some bits from a BitVec

    • Concat: Concatenate BitVecs

  • Z3 operators need operands of the same size ; Extract/Concat/ZeroSignExt can help you to meet this requirement

Z3py tips: RotateRight/Left

  • Equivalent of x86's ROL/ROR instructions

Z3py tips: prove

  • Another quite cool & important function is prove

  • The function basically checks the given equation is always true

  • If not proven, Z3 will give you a counterexample

  • Example: Let's prove that Concat works properly

Z3py tips: prove example II

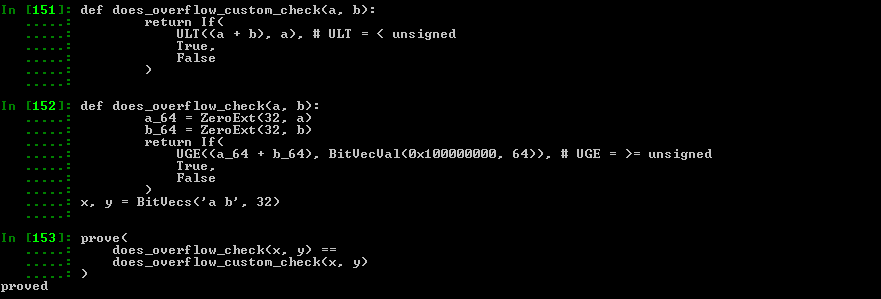
  • More real example:

    • Can we use ((a + b) < a) to know if there is an overflow when adding unsigned 32 bits integers a and b?

    • Instead of storing the result in a 64 bits integer & checking that the result is not >= 0x100000000?

  • proof_unsigned_integer_overflow_chech.py

                            def does_overflow_custom_check(a, b):
    return If(
        ULT((a + b), a), # ULT = < unsigned
        True,
        False
    )

def does_overflow_check(a, b):
    a_64 = ZeroExt(32, a)
    b_64 = ZeroExt(32, b)
    return If(
        UGE((a_64 + b_64), BitVecVal(0x100000000, 64)), # UGE = >= unsigned
        True,
        False
    )
x, y = BitVecs('a b', 32)

prove(
    does_overflow_check(x, y) ==
    does_overflow_custom_check(x, y)
)

Z3py tips: prove example II

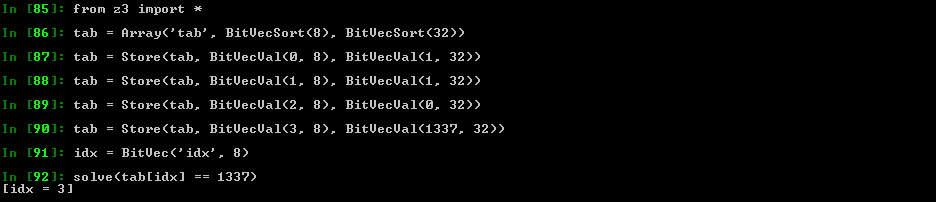
Z3py tips: Arrays

  • Quite handy to simulate the memory in a symbolic way

  • Z3 will use a brute-force approach, it will essentially try all possible combinations. It will not manage to find the "smart" proof that we (as humans) immediately see.

  • You can access the array content with [] or Select, and write to it via Store

Z3py tips: substitute

  • This function allows you to substitute variables by whatever you want in an expression

  • You can replace a symbolic variable by a concrete value

  • Or the way around

Z3Py tips: And/Or/Distinct

  • Equivalent to Python's and & or

  • They are really nice to use: you can give them an array of expressions, or inlined expressions

  • A lot of time you need to express the following: "I want all my symbolic variables to be different"

    • You can do it manually via And(x1 != x2, x2 != x3, x1 != x3)

    • Or you can use Distinct(x1, x2, x3) which is way cleaner

Z3Py tips: If

  • It is sometimes useful, but it's not like Python's if & else

  • Different how? Not really easy to explain

  • Here is a C code / Z3 example: 

                                        
unsigned int a, b;
if((a + b) < 100)
{
    a += 100;
    b -= 10;
}
else
{
    a = 1337;
    b += 1000;
}

Z3Py tips: Visiting Z3 expressions

  • You may need to inspect & visit the AST of a Z3 expression

    • Useful for transformation, conversion, etc.

    • The expression is a tree

  • e.arg(x) gets you the x th argument in the expression

  • e.num_args() gives you the number of argument

  • Check z3topy.py

Z3Py toys: graph coloring

Z3Py toys: NQueens

Z3Py toys: Mojette

Z3Py toys: Magic square

References

Conclusion

  • Z3 is really powerful, use it!

  • There are loads of advanced features that I don't use / I don't know how to use:

    • Tactics / Strategies / Subgoals?

    • Functions?

    • Patterns?

    • Data-types?

    • Quantifiers?

  • If you don't like Z3's API and / or its features try out another one:

Symbolic execution 101

Symbolic execution: definition with words

  • Symbolic execution involves computation of a mathematical expression that represents the logic within a program. It can be thought of as an algebra designed to express computation.
    Richard @richinseattle Johnson, NSC 2014

  • An analogy I like to give between concrete / symbolic execution and mathematical functions:
    • Concrete execution would be to know that f(3) = 19
    • Symbolic execution would be to know that f(x) = x**2 + 10

  • Symbolic execution expresses every concrete executions possible

Symbolic execution: definition with words II

  • So does that mean I have to recode a virtual CPU with the semantic of every instructions?

  • Nope ; see it as a recipe. Take shortcuts to make your life easier:
    • I don't need to handle branches
    • I only need to handle 4 different instructions
    • Think about the granularity you want: a basic block, a function, a library, an entire program
    • Why not symbolically execute intermediate representation code instead of assembly?

Symbolic execution: definition with code

  • Let's imagine this code

                                    void hello(unsigned char c)
{
    unsigned char win;
    unsigned int a = c;
    a = a*2 + 0xdeadbeef;
    if(a >= 0 && a < 0xbaad)
        win = 1;
    else
        win = 0;
}
  • Concrete:

  • c = 0xf0
  • a = 0x000000f0
  • a = 0xdeadc0cf

  • win = 0
  • Symbolic:

  • c is an input sym var
  • a_0 = ZeroExt(24, c)
  • a = a_0*2 + 0xdeadbeef

  • win = If(And(UGE(a, 0), ULT(a, 0xbaad)), 1, 0)

References

Practical reverse-engineering

Breaking weak hash function: hash collisions

  • Original blog-post by James '@tiraniddo' Forshaw: Generating hash collisions

  • The problem in details ; bear with me:
    • Goals
      • s = "abc\0" + SUFFIX
      • H(s) == H("xyz")
      • strcmp(s, "abc") == 0
    • Definitions
      • SUFFIX is a string fully controlled: even non-ASCII characters are allowed
      • H is a hashing function

    • Let's even find an ASCII printable SUFFIX!

Breaking weak hash function: hash collisions

  • Modeling C concrete strings
    • Sequence of BitVecVal8
      •                                     def str_to_BitVecVals8(s):
    return map(
        lambda x: BitVecVal(ord(x), 8),
        list(s)
    )
  • Modeling ASCII-printable C symbolic strings
    • Sequence of BitVec8                                                                       
      •                                     def ascii_printable(x):
    return And(0x20 <= x, x <= 0x7f)

def generate_ascii_printable_string(base_name, size, solver):
    bytes = [BitVec('%s%d' % (base_name, i), 8) for i in range(size)]
    solver.add(And(map(ascii_printable, bytes)))
    return bytes

Breaking weak hash function: hash collisions

  • Modeling H                                                                       
    •                                 def H(input_bytes):
    h = 0
    for byte in input_bytes:
        h = h * 31 + ZeroExt(24, byte)
    return h

Breaking weak hash function: hash collisions

  • Putting it all together: 
    •                                 def collide(target_str, base_str):
    size_suffix = 7
    s = Solver()
    res = str_to_BitVecVals8(base_str) + [BitVecVal(0, 8)] + generate_ascii_printable_string('res', size_suffix, s)
    s.add(H(res) == H(str_to_BitVecVals8(target_str)))
    if s.check() == sat:
        x = s.model()
        return base_str + '\x00' + ''.join(chr(x[i].as_long()) for i in res[-size_suffix:])
    raise Exception('Unsat!')

def main(argc, argv):
    a = 'xyz'
    b = 'abc'
    c = collide(a, b)
    print 'c = %r' % c
    print 'H(%r) == H(%r)' % (a, c)
    print 'strcmp(%r, %r) = 0' % (c, b)

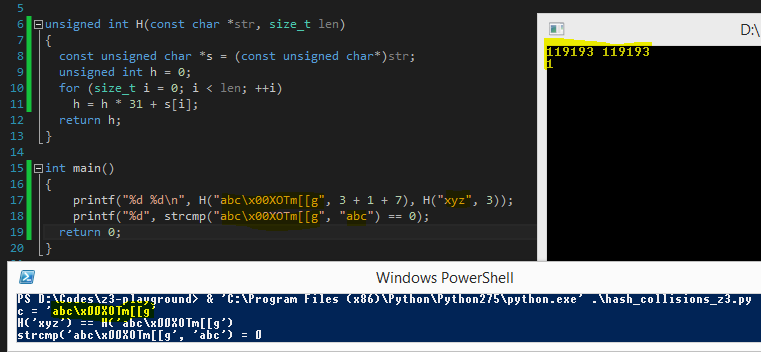
Breaking weak hash function: hash collisions

  • Job done!
  • No brute-force, elegant solution: didn't even thought at how we could have "reversed" H, Z3 did it for us
  • Full code is here: hash_collisions_z3.py

Breaking conservative semantic obfuscation: Kryptonite

  • Kryptonite is an LLVM optimization pass that adds semantic-preserving obfuscation for arithmetic operations

    • PoC I've written up in "Obfuscation of steel: meet my Kryptonite" back in 2013

    • Doing the transformation at the LLVM IR level allows you to support every LLVM back-end architecture: ARM, x86, x64 & a lot of others

    • It also means you can write your code in every languages supported by LLVM

    • And obviously, you can output binaries in whatever executable formats LLVM supports: Elf, Mach-o, PE

    • Check out O-LLVM if you are interested in this field

  • The semantic of the program is preserved: the assembly is just a bit disturbing

Breaking conservative semantic obfuscation: Kryptonite

                            
unsigned int add(unsigned int a, unsigned int b)
{
    return a + b;
}

int main(int argc, char* argv[])
{
    if(argc != 3)
        return 0;

    printf("Result: %u\n", add(atoll(argv[1]), atoll(argv[2])));
    return 1;
}
                        
                            $ wget https://raw.github.com/0vercl0k/stuffz/master/llvm-funz/kryptonite/llvm-functionpass-kryptonite-obfuscater.cpp
$ clang++ llvm-functionpass-kryptonite-obfuscater.cpp `llvm-config --cxxflags --ldflags --libs core` -shared -o llvm-functionpass-kryptonite-obfuscater.so
$ clang -S -emit-llvm add.c -o add.ll
$ opt -S -load ~/dev/llvm-functionpass-kryptonite-obfuscater.so -kryptonite -heavy-add-obfu add.ll -o add.opti.ll && mv add.opti.ll add.ll
$ opt -S -load ~/dev/llvm-functionpass-kryptonite-obfuscater.so -kryptonite -heavy-add-obfu add.ll -o add.opti.ll && mv add.opti.ll add.ll
$ llc -O0 -filetype=obj -march=x86 add.ll -o add.o
$ clang -static add.o -o kryptonite-add
$ strip --strip-all ./kryptonite-add

Breaking conservative semantic obfuscation: Kryptonite

                            PS C:\Users\0vercl0k> dir D:\Codes\llvm-funz\kryptonite-add
Length Name
------ ----
689112 kryptonite-add

Breaking conservative semantic obfuscation: Kryptonite

  • The context

    • We want to attack a single basic block

    • If you look closer at the previous slide, only a subset of x86's instructions are used

      • Their semantics are easy to implement

    • We don't need to handle branches, nor EFLAGS

    • We don't know the number of input symbolic variables

      • Heuristic: Every time we read from an uninitialized location, we treat it as an input variable

  • The plan

    • Symbolically execute the basic block

    • To do so you need a virtual environment: both CPU & memory

    • For us, virtual CPU = bunch of registers that can either hold symbolic variables or concrete values

Breaking conservative semantic obfuscation: Kryptonite

  • tiny_symbolic_execution_engine_z3.py:

    • A disassembler class

      • We need to parse the code to execute: IDAPython, string manipulation

    • A virtual CPU: the core of the program

      • Use the disassembler component & implement the instruction semantics

      • Also simulates memory

      • Keep track of the (simplified) equations

                            Launching the engine..
Trying to read a non-initialized area, we got a new symbolic variable: arg0
Trying to read a non-initialized area, we got a new symbolic variable: arg1
Done, retrieving the equation in EAX, and simplifying..

Breaking conservative semantic obfuscation: Kryptonite

                            EAX=(~(Concat(2147483647, Extract(0, 0, arg1)) |
   Concat(2147483647, ~Extract(0, 0, arg0)) |
   4294967294) |
 ~(Concat(2147483647, ~Extract(0, 0, arg1)) |
   Concat(2147483647, Extract(0, 0, arg0)) |
   4294967294)) +
Concat(~(Concat(1073741823, Extract(1, 1, arg1)) |
         Concat(1073741823, ~Extract(1, 1, arg0)) |
         Concat(1073741823,
                ~(~Extract(0, 0, arg1) |
                  ~Extract(0, 0, arg0)))) |
       ~(Concat(1073741823, ~Extract(1, 1, arg1)) |
         Concat(1073741823, Extract(1, 1, arg0)) |
         Concat(1073741823,
                ~(~Extract(0, 0, arg1) |
                  ~Extract(0, 0, arg0)))) |
       ~(Concat(1073741823, Extract(1, 1, arg1)) |
         Concat(1073741823, Extract(1, 1, arg0)) |
         Concat(1073741823, ~Extract(0, 0, arg1)) |
         Concat(1073741823, ~Extract(0, 0, arg0)) |
         2147483646) |
       ~(Concat(1073741823, ~Extract(1, 1, arg1)) |
         Concat(1073741823, ~Extract(1, 1, arg0)) |
         Concat(1073741823, ~Extract(0, 0, arg1)) |
         Concat(1073741823, ~Extract(0, 0, arg0)) |
         2147483646),
       0) +
...

  • Not quite what I expected but as I mentioned before, simplification strategies are not magic ; complicated problem

    • Read Rolf's answer if you want to know why

Breaking conservative semantic obfuscation: Kryptonite

  • But we can eventually prove it is equivalent to arg0 + arg1 & then replace the expression with the simplified version right?

                            
def _simplify_additions(self, eq):
    # The two expressions are equivalent ; we got a simplification!
    if prove(Sum(self.sym_variables) == eq):
        return Sum(self.sym_variables)

    return eq

def get_reg_equation_simplified(self, reg):
    eq = self.get_reg_equation(reg)
    eq = simplify(self._simplify_additions(eq))
    return eq
#[..]
    print sym.get_reg_equation_simplified('eax')

                            Launching the engine..
Trying to read a non-initialized area, we got a new symbolic variable: arg0
Trying to read a non-initialized area, we got a new symbolic variable: arg1
Done, retrieving the equation in EAX, and simplifying..
EAX=arg0 + arg1
Job done, more details here if you want

Finding ROP gadgets with constraints

  • The context

    • ROP gadget = relatively small sequence of instructions that ends with a branching instruction

    • Is "xor eax, eax ; ret" equals to "mov eax, 0xffffffff ; inc eax ; ret"?

      • They are not stricly equal, nope

      • Why? EFLAGS.AF for example

      • What if we care only about the state of EAX after the gadget execution?

        • In that case they are equivalent!

    • The gadgets are small & they usually only use a small subset of x86 instructions: we don't really care about: SSE/MMX or crazy instructions

    The problem

    • To be able to compare gadgets, we need instruction semantics ; where do we get that for free?

Finding ROP gadgets with constraints

  • The solution

    • Introducing amoco a Python framework for static program analysis developed by Axel '@bdcht' Tillequin

    • Symbolic execution engine for x86, x64, ARM & instruction semantics

      • Uses its own expression mechanism so far

      • Most of important (for us) x86 instructions are implemented

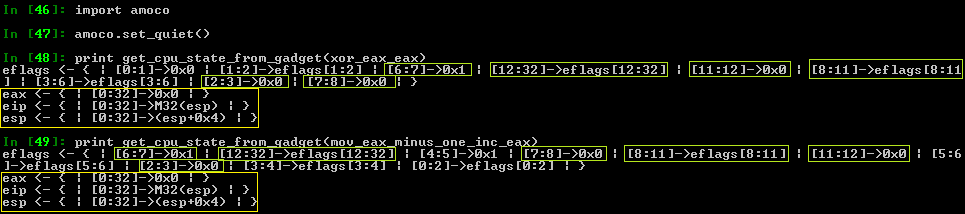
Finding ROP gadgets with constraints

  • The plan

    • Symbolically execute gadgets with amoco

    • Because it uses its own "expression" classes, we need to sort of convert that in Z3

      • @bdcht plans to integrate Z3 in his framework at some point

        • No more magic ugly tricks to go from one to another

    • Then we are free to compare the state of the two virtual CPUs

    • You can actually even set / add your own constraints

Finding ROP gadgets with constraints

  • look_for_gadgets_with_equations.py:

    • What it looks like in the code:

      • "I want EAX = EBX = 0 at the end of the gadget execution"

                                                            
cpu_state_end_target.wants_register_equal('eax', 0)
cpu_state_end_target.wants_register_equal('ebx', 0)

      • "I want ((ESP >= ESP + 1000) && (ESP < ESP + 2000)) && (EAX == 0)"

                                                            
cpu_state_end_target.wants_register_greater_or_equal('esp', cpu.esp + 1000)
cpu_state_end_target.wants_register_lesser('esp', cpu.esp + 2000)
cpu_state_end_target.wants_register_equal('eax', 0)

      • "I want EIP = ESP at the end of the gadget execution"

                                                            
cpu_state_end_target.wants_register_equal('eip', 'esp')

Finding ROP gadgets with constraints

  • look_for_gadgets_with_equations.py:

    • Example of cool results:

      • "I want EAX = EBX = 0 at the end of the gadget execution"

                                                            
xor eax, eax ; push eax ; mov ebx, eax ; ret
xor eax, eax ; xor ebx, ebx ; ret

      • "I want ((ESP >= ESP + 1000) && (ESP < ESP + 2000)) && (EAX == 0)"

                                                            
xor eax, eax ; add esp, 0x45c ; pop ebx ; pop esi ; pop edi ; pop ebp ; ret

      • "I want EIP = ESP at the end of the gadget execution"

                                                            
add dword ptr [ebx], 2 ; push esp ; ret 
jmp esp
pushad ; mov eax, 0xffffffff ; pop ebx ; pop esi ; pop edi ; ret

Taming a wild MIPS binary

  • The context

    • NoSuchCon 2014 crack-me (the first of the three challenges) coded by @elvanderb

    • ELF MIPS binary protected by nanomites

      • Father debugs the son ; Father's code is called each time the son executes break (equivalent of int3)

      • Father modifies the son's CPU context to obfuscate the execution flow: the son won't be executed as it appears in IDA

    • The protection scheme:

      • Serial of 24 bytes

      • win = memcmp(F(serial_entered), '[ Synacktiv + NSC = <3 ]') == 0

Taming a wild MIPS binary

  • Long story short:

    • The father uses an algorithm to know where it has to redirect his son

      • Once we have it, we know in which order the son is going to execute its code

    • The son uses an algorithm to "decrypt" the serial (6 DWORDs)

      • Each DWORD is modified in place ; each DWORD is modified in a different way thanks to the father

      • Once we figure out the way each DWORD is modified, we can reverse it & break the challenge

Taming a wild MIPS binary

Taming a wild MIPS binary

  • The plan:

    • Symbolicly execute the three or four big basic blocks we need

    • Then ask Z3 to find the input required to have F(serial) = '[ Synacktiv + NSC = <3 ]'

    • We don't need branches & only need to implement < 20 instruction in our virtual CPU

    • Most instructions are about basic mathematical computations: easy to implement with Z3

    • Memory simulation with a simple array

    • We can use our code both as a simplistic MIPS emulator (with concrete values)..

    • ..or as a symbolic execution engine (with symbolic variables)

    • All of that in less than 500 lines of Python

Taming a wild MIPS binary

  • The plan:

    • Once we have an engine working:

      • We can use it to recover the father algorithm

        • Execution flow deobfuscation: we have now the code of the son unscrambled / clean

      • We can use it to recover the son algorithm

        • Ask Z3 the correct input values & job done!

    • All of that in less than 300 lines of Python

Taming a wild MIPS binary

  • What the first DWORD looks after all the modification:

                            
; input_dword_0
(declare-fun a () (_ BitVec 32))
(let ((?x966 ((_ extract 31 30) (bvadd (_ bv1169698645 32) (bvnot a)))))
(let ((?x991 ((_ extract 4 4) (bvadd (_ bv21 5) (concat (bvadd (_ bv5 3) (bvnot ((_ extract 2 0) a))) ?x966)))))
(let ((?x999 (bvnot ?x991)))
(let ((?x952 ((_ extract 15 5) (bvadd (_ bv35861 16) (concat (bvadd (_ bv12117 14) (bvnot ((_ extract 13 0) a))) ?x966)))))
(let ((?x1002 (concat ((_ extract 29 27) (bvadd (_ bv1169698645 32) (bvnot a))) (bvadd (_ bv95956821 27) (bvnot ((_ extract 26 0) a))) ?x966)))
(let ((?x980 (bvadd (_ bv3493170197 32) ?x1002)))
(let ((?x1003 (concat (bvnot (bvadd (_ bv5 4) (concat (bvadd (_ bv1 2) (bvnot ((_ extract 1 0) a))) ?x966))) (bvnot ((_ extract 31 17) ?x980)) (bvnot ((_ extract 16 16) ?x980)) (bvnot ?x952) ?x999)))
(let ((?x1008 (bvadd (_ bv422262738 32) ?x1003)))
(let ((?x1017 (concat (bvnot ((_ extract 26 17) ?x980)) (bvnot ((_ extract 16 16) ?x980)) (bvnot ?x952) ?x999)))
(let ((?x1018 (bvadd (_ bv2832338 23) ?x1017)))
(let ((?x1085 (concat (bvnot ((_ extract 22 21) ?x1018)) ((_ extract 20 17) ?x1018) (bvnot ((_ extract 16 16) ?x1018)) ((_ extract 15 15) ?x1018) (bvnot ((_ extract 14 14) ?x1018)) ((_ extract 13 12) ?x1018) (bvnot ((_ extract 11 11) ?x1018)) ((_ extract 10 10) ?x1018) (bvnot ((_ extract 9 7) ?x1018)) ((_ extract 6 6) ?x1018) (bvnot ((_ extract 5 5) ?x1018)) ((_ extract 4 4) ?x1018) (bvnot ((_ extract 3 1) ?x1018)) ?x999 ((_ extract 31 31) ?x1008) (bvnot ((_ extract 30 30) ?x1008)) ((_ extract 29 29) ?x1008) (bvnot ((_ extract 28 28) ?x1008)) ((_ extract 27 25) ?x1008) (bvnot ((_ extract 24 23) ?x1008)))))
(let ((?x1025 (concat (bvadd (_ bv12 4) (concat ((_ extract 26 25) ?x1008) (bvnot ((_ extract 24 23) ?x1008)))) ((_ extract 31 4) (bvadd (_ bv1338037900 32) ?x1085)))))
(let ((?x984 (bvnot ((_ extract 17 17) (bvadd (_ bv2036738909 32) ?x1025)))))
(let ((?x1001 (concat (bvnot (bvadd (_ bv11101 17) ((_ extract 20 4) (bvadd (_ bv1338037900 32) ?x1085)))) (bvnot ((_ extract 31 17) (bvadd (_ bv2036738909 32) ?x1025))))))
(let ((?x1010 (bvadd (_ bv3562860298 32) ?x1001)))
(let ((?x1004 (bvnot ((_ extract 1 1) ?x1010))))
(let ((?x1201 ((_ extract 3 3) (bvadd (_ bv6 5) (concat (bvnot ((_ extract 4 4) ?x1010)) ((_ extract 3 2) ?x1010) ?x1004 ?x984)))))
(let ((?x1196 ((_ extract 4 4) (bvadd (_ bv6 5) (concat (bvnot ((_ extract 4 4) ?x1010)) ((_ extract 3 2) ?x1010) ?x1004 ?x984)))))
(let ((?x1020 (concat ((_ extract 31 31) ?x1010) (bvnot ((_ extract 30 30) ?x1010)) ((_ extract 29 29) ?x1010) (bvnot ((_ extract 28 28) ?x1010)) ((_ extract 27 27) ?x1010) (bvnot ((_ extract 26 25) ?x1010)) ((_ extract 24 23) ?x1010) (bvnot ((_ extract 22 22) ?x1010)) ((_ extract 21 17) ?x1010) (bvnot ((_ extract 16 13) ?x1010)) ((_ extract 12 12) ?x1010) (bvnot ((_ extract 11 11) ?x1010)) ((_ extract 10 9) ?x1010) (bvnot ((_ extract 8 4) ?x1010)) ((_ extract 3 2) ?x1010) ?x1004 ?x984)))
(let ((?x1061 (bvadd (_ bv4035799430 32) ?x1020)))
(let ((?x1206 (concat (bvnot ((_ extract 2 2) (bvadd (_ bv6 3) (concat ((_ extract 2 2) ?x1010) ?x1004 ?x984)))) ((_ extract 1 1) (bvadd (_ bv6 3) (concat ((_ extract 2 2) ?x1010) ?x1004 ?x984))) ((_ extract 17 17) (bvadd (_ bv2036738909 32) ?x1025)) ((_ extract 31 30) ?x1061) (bvnot ((_ extract 29 29) ?x1061)) ((_ extract 28 27) ?x1061) (bvnot ((_ extract 26 25) ?x1061)) ((_ extract 24 22) ?x1061) (bvnot ((_ extract 21 21) ?x1061)) ((_ extract 20 16) ?x1061) (bvnot ((_ extract 15 15) ?x1061)) ((_ extract 14 12) ?x1061) (bvnot ((_ extract 11 9) ?x1061)) (bvnot ((_ extract 8 8) ?x1061)) ((_ extract 7 7) ?x1061) (bvnot ((_ extract 6 6) ?x1061)) (bvnot ((_ extract 5 5) ?x1061)) ?x1196 (bvnot ?x1201))))
(let ((?x1043 (bvadd (_ bv3499560052 32) ?x1206)))
(let ((?x1230 ((_ extract 14 13) ?x1043)))
(let ((?x1223 (concat (bvnot ((_ extract 12 12) ?x1043)) ((_ extract 11 11) ?x1043) (bvnot ((_ extract 10 10) ?x1043)) ((_ extract 9 9) ?x1043) (bvnot ((_ extract 8 7) ?x1043)) ((_ extract 6 6) ?x1043) (bvnot ((_ extract 5 5) ?x1043)) ((_ extract 4 3) ?x1043) (bvnot ((_ extract 2 2) ?x1043)) ((_ extract 1 1) ?x1043) (bvnot ?x1201) (bvnot ((_ extract 31 30) ?x1043)) ((_ extract 29 28) ?x1043) (bvnot ((_ extract 27 27) ?x1043)) ((_ extract 26 25) ?x1043) (bvnot ((_ extract 24 15) ?x1043)) ?x1230)))
(let ((?x1005 (bvadd (_ bv2171031339 32) ?x1223)))
(let ((?x1229 (concat (bvnot ((_ extract 14 13) ?x1005)) (bvnot ((_ extract 12 12) ?x1005)) (bvnot ((_ extract 11 11) (bvadd (_ bv3883 12) (concat (bvnot ((_ extract 24 15) ?x1043)) ?x1230)))) ((_ extract 10 8) (bvadd (_ bv3883 12) (concat (bvnot ((_ extract 24 15) ?x1043)) ?x1230))) (bvnot ((_ extract 7 5) (bvadd (_ bv3883 12) (concat (bvnot ((_ extract 24 15) ?x1043)) ?x1230)))) ((_ extract 4 3) (bvadd (_ bv3883 12) (concat (bvnot ((_ extract 24 15) ?x1043)) ?x1230))) (bvnot ((_ extract 2 1) (bvadd (_ bv3 3) (concat (bvnot ((_ extract 15 15) ?x1043)) ?x1230)))) (bvnot (bvadd (_ bv1 1) ((_ extract 13 13) ?x1043))) (bvnot ((_ extract 31 30) ?x1005)) ((_ extract 29 22) ?x1005) (bvnot ((_ extract 21 21) ?x1005)) ((_ extract 20 20) ?x1005) (bvnot ((_ extract 19 19) ?x1005)) ((_ extract 18 16) ?x1005) (bvnot ((_ extract 15 15) ?x1005)))))
(let ((?x1132 (concat ((_ extract 23 22) ?x1005) (bvnot ((_ extract 21 21) ?x1005)) ((_ extract 20 20) ?x1005) (bvnot ((_ extract 19 19) ?x1005)) ((_ extract 18 16) ?x1005) (bvnot ((_ extract 15 15) ?x1005)))))
(concat ((_ extract 28 9) (bvadd (_ bv2400525917 32) ?x1229)) (bvadd (_ bv93 9) ?x1132) ((_ extract 31 29) (bvadd (_ bv2400525917 32) ?x1229))))))))))))))))))))))))))))))

Taming a wild MIPS binary

                            
PS D:\Codes\NoSuchCon2014> python .\solve_nsc2014_step1_z3.py
==================================================
> Instantiating the symbolic execution engine..
> Generating dynamically the code of the son & reorganizing / cleaning it..
> Configuring the virtual environment..
> Running the code..
> Instantiating & configuring the solver..
> Solving..
> Constraints solvable, here are the 6 DWORDs:
 a = 0xFE446223
 b = 0xBA770149
 c = 0x75BA5111
 d = 0x78EA3635
 e = 0xA9D6E85F
 f = 0xCC26C5EF
> Serial: 322644EF941077AB1115AB575363AE87F58E6D9AFE5C62CC
==================================================

root@debian-mipsel:~# /home/user/crackmips 322644EF941077AB1115AB575363AE87F58E6D9AFE5C62CC
good job!
Next level is there: http://nsc2014.synacktiv.com:65480/oob4giekee4zaeW9/

Taming a wild MIPS binary

References

Conclusion

  • Symbolic execution & theorem provers are really two useful / powerful tools for security / reverse-engineering tasks

  • The deck of slides will be available online

  • Feel free to reach out to me via email / twitter for any questions and / or feedbacks

  • Big thanks to SecurityDay for having me :-)

  • "My proof readers are awesome" (c) Rolf, 2014

Shameless plug: Diary of a reverse-engineer

We are always looking for cool posts / articles, feel free to reach out to us!

Diary of a reverse-engineer, @doar_e

@jonathansalwan, @__x86, @0vercl0k

Questions?