Introduction

About two weeks ago, my friend mongo challenged me to solve a reverse-engineering puzzle put up by the SSD team for OffensiveCon2018 (which is a security conference that took place in Berlin in February). The challenge binary is available for download here and here is one of the original tweet advertising it.

With this challenge, you are tasked to reverse-engineer a binary providing some sort of encryption service, and there is supposedly a private key (aka the flag) to retrieve. A remote server with the challenge running is also available for you to carry out your attack. This looked pretty interesting as it was different than the usual keygen-me type of reverse-engineering challenge.

Unfortunately, I didn't get a chance to play with this while the remote server was up (the organizers took it down once they received the solutions of the three winners). However, cool thing is that you can easily manufacture your own server to play at home.. which is what I ended up doing.

As I thought the challenge was cute enough, and that I would also like to write on a more regular basis, so here is a small write-up describing how I abused the server to get the private key out. Hope you don't find it too boring :-).

Playing at home

Before I start walking you through my solution, here is a very simple way for you to set it up at home. You just have to download a copy of the binary here, and create a fake encryption library that exports the encrypt/decrypt routines as well as the key material (private_key / private_key_length):

#include <stdio.h>
#include <stdint.h>
#include <inttypes.h>

uint32_t number_of_rows = 16;
uint32_t private_key_length = 32;
uint8_t private_key[32] = { 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0 };

const uint64_t k = 0xba0bab;

uint64_t decrypt(uint64_t x) {
    printf("decrypt(%" PRIx64 ") = %" PRIx64 "\n", x, x ^ k);
    return x ^ k;
}

uint64_t encrypt(uint64_t y) {
    printf("encrypt(%" PRIx64 ") = %" PRIx64 "\n", y, y ^ k);
    return y ^ k;
}

The above file can be compiled with the below command:

$ clang++ -shared -o lib.so -fPIC lib.cc

Dropping the resulting lib.so shared library file inside the same directory as the challenge should be enough to have it properly run. You can even hook it up to a socket via socat to simulate a remote server you have to attack:

$ socat -vvv TCP-LISTEN:31337,fork,reuseaddr EXEC:./cha1

If everything worked as advertised, you should now be able to interact with the challenge remotely and be greeted by the below menu when connected to it:

Please choose your option:
0. Store Number
1. Get Number
2. Add
3. Subtract
4. Multiply
5. Divide
6. Private Key Encryption
7. Binary Representation
8. Exit

Off you go have fun now :)

Recon

When I start looking at a challenge I always spend time to understand a bit more of the story around it. This both gives me direction as well as helps me identify pitfalls. For example here, the story tells me that we have a secret to exfiltrate and focusing the analysis on the code interacting / managing this secret sounds like a good idea. The challenge was also advertised as a reverse-engineering task so I didn't really expect any pwning. A logical flaw, design issue or a very constrained memory corruption type of issue is what I was looking for.

Once base64-decoded, the binary is a 10KB (small) unprotected ELF64. The binary is PIE and imports a bunch of data / functions from a file named lib.so that we don't have access to. Based on the story we have been given, we can expect both the key materials and the encryption / decryption routines stored there.

extern:0000000000202798 ; _QWORD __cdecl decrypt(unsigned __int64)
extern:0000000000202798                 extrn _Z7decryptm:near  ; DATA XREF: .got.plt:off_202020↑o
extern:00000000002027A0 ; _QWORD __cdecl encrypt(unsigned __int64)
extern:00000000002027A0                 extrn _Z7encryptm:near  ; DATA XREF: .got.plt:off_202028↑o

Even though the challenge seems to use C++ and the STL, the disassembled / decompiled code is very easy to read so it doesn't take a whole lot of time to understand a bit more what this thing is doing.

According to what the menu says, it looks like a store of numbers; whatever that means. Quick reverse-engineering of the getter and setter functions we learn a bit more of what is a number. First, every number (number_t) being stored is encrypted when inserted into the store, and decrypted when retrieved out of the store.

uint64_t write_number_to_store(number_t *number2write, uint64_t value, bool encrypted)
{
    uint64_t encrypted_val = value;
    if(encrypted) {
    encrypted_val = encrypt(value);
    }

    size_t bitidx = 31LL;
    do
    {
    uint8_t curr_encrypted_val = encrypted_val;
    encrypted_val >>= 1;
    number2write->bytes[bitidx--] = curr_encrypted_val & 1;
    } while ( bitidx != -1 );
    return encrypted_val;
}

Interestingly, the third argument of the function allows you to write a clear-text number into the store but it is apparently not used anywhere in the challenge.. oh well :)

Once the numbers are encrypted, they also get encoded with a very simple transformation: every bit is written to a byte (0 or 1). As the numbers being stored are 32 bits integers, naturally the store needs 32 bytes per number.

00000000 number_t        struc ; (sizeof=0x20)
00000000 bytes           db 32 dup(?)
00000020 number_t        ends

After looking a bit more at the other options, and with the above in mind, it is pretty straightforward to recover part of the structure that keeps the global state of the store (state_t). The store has a maximum capacity of 32 slots, the current size of the store is stored in the lower 5 bits (2**5 = 32) of some sort of status variable. At this point I started drafting the structure state_t:

00000000 state_t         struc ; (sizeof=0x440, align=0x8)
00000000 numbers         number_t 32 dup(?)
00000400 pkey            dq ?
00000408 size            db ?
00000409                 db ? ; undefined
0000040A                 db ? ; undefined
0000040B                 db ? ; undefined
0000040C                 db ? ; undefined
0000040D                 db ? ; undefined
0000040E                 db ? ; undefined
0000040F                 db ? ; undefined
00000410 x               dw ?
00000412 xx              db 38 dup(?)
00000438 xxx             dq ?
00000440 state_t         ends

The Private Key Encryption function is the one that looked a bit more involved than the others. But as far as I was concerned, it was doing ""arithmetic"" on numbers that you previously had stored: one called the message and one called the key.

Before actually starting to look for issues, I needed to answer two questions:

1. Where is the key stored?
2. What prevents me from accessing it?

By looking at the store initialization code we can answer the first question. The content of private_key is put inside the store in the slot number_of_rows + 2. Right after, the size of the store is set to number_of_rows. The net result of this operation being - assuming proper bounds-checking from all the commands interacting with the store - that the user cannot access the key directly.

Finding the needle: getting access to the key material

Fortunately for us there's not that much code, so auditing every command is easy enough. All the commands actually do a good job at sanitizing things at first sight. Every time the application asks for a slot index, it is bounds-checked against the store size before getting used. It even throws an out-of-range exception if you are trying to access an out-of-bounds slot. Here is an example with the divide operation (number_store is the global state, NumberOfNumbers is a mask extracting the lower 5 bits of the size field to compute the current size of the store):

const uint32_t NumberOfNumbers = 0x1F;
case Divide:
    arg1_row = 0LL;
    arg2_row = 0LL;
    result_row = 0LL;
    std::cout << "Enter row of arg1, row of arg2 and row of result" << std::endl;
    std::cin >> arg1_row;
    std::cin >> arg2_row;
    std::cin >> result_row;
    store_size = number_store->size & NumberOfNumbers;
    if(arg1_row >= store_size || arg2_row >= store_size || result_row >= store_size)
        goto OutOfRange;

There's a catch though. If we look closer at every instance of code that interacts with the size field of the store there is something a bit weird going on.

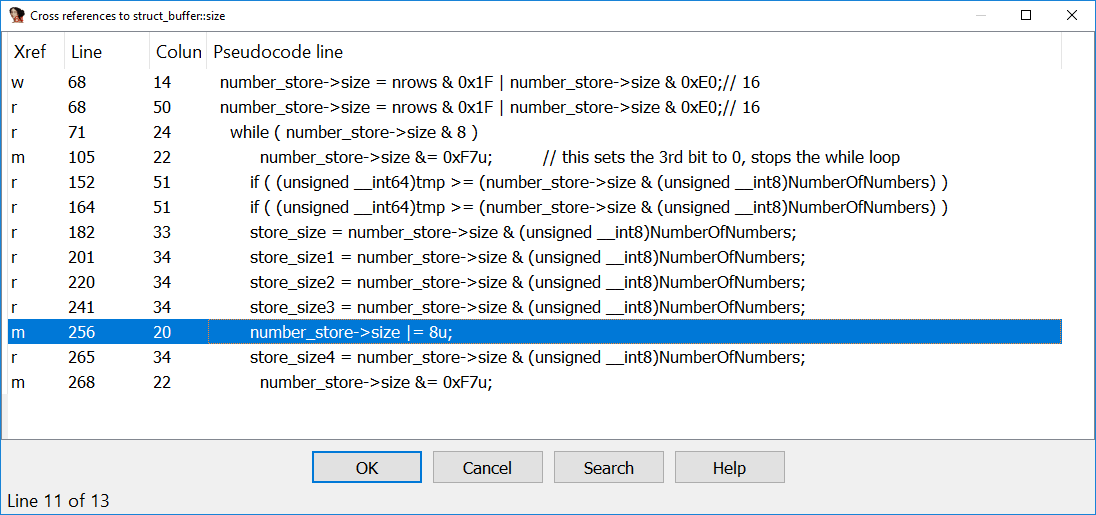
In the above screenshot you can see that the highlighted cross-reference looks a bit odd as it is actually changing the size by setting the bit number three (0b1000). If we pull the code for this function we can see the below:

case PrivateKeyEncryption:
    number_store->size |= 8u;
    msg_row = 0uLL;
    key_row = 0uLL;
    std::cout << "Enter row of message, row of key" << std::endl;
    std::cin >> msg_row;
    std::cin >> key_row;
    store_size = number_store->size & NumberOfNumbers;
    if(msg_row >= store_size || key_row >= store_size) {
    number_store->size &= 0xF7u;
    std::cout << "Row number is out of range" << std::cout;

I completely overlooked this detail at first as this bit is properly cleared out on error (with the 0xF7 mask). This bit also sounded to be used as a switch to start or stop the encryption process. I could clearly see it used in the encryption loop like in the below:

while(number_store->size & 8) {
    // do stuff
    std::cout << "Continue Encryption? (y/n)" << std::endl;
    std::cin >> continue_enc;
    if(continue_enc == 'Y' || continue_enc == 'y') {
    // do encryption..stuff
    } else if(continue_enc == 'n' || continue_enc == 'N') {
    number_store->size &= 0xF7u;
    }

The thing is, as this bit overlaps with the 5th bit of the store size, setting it also means that we can now access slots from index 0 up to slot 0x10|8=0x18. If the previous is a bit confusing, consider the following C structure:

union {
    struct {
        size_t x : 3;
        size_t bit3 : 1;
    } s1;
    size_t store_size : 5;
} size = {};

And as we said a bit earlier the key material is stored in the slot number_of_rows + 2 = 0n18.

__int64 realmain(struct_buffer *number_store) {
    nrows = number_of_rows;
    pkey_length = private_key_length;
    pkey = &number_store->numbers[number_of_rows + 2];
    is_pkey_empty = private_key_length == 0;
    number_store->pkey = pkey;
    if(!is_pkey_empty) {
    memmove(pkey, &private_key, pkey_length);
    }
    number_store->pkey->bytes[pkey_length - 1] |= 1u;
    number_store->size = nrows & 0x1F | number_store->size & 0xE0;
    // ...

Cool beans, I guess we now have a way to have the application interact with the slot containing the private key which sounds like... progress, right?

Bending the needle: building an oracle

Being able to access the key through the private key encryption feature is great, but it also doesn't give us much just yet. We need to understand a bit more what this feature is doing before coming up with a way to abuse it. After spending a bit of time reverse-engineering and debugging it, I've broken down its logic into the below steps:

1. The user enters the slot of the message and the slot of the key (either or both of these slots can be the private key slot),
2. The number stored into the key slot is copied into the global state; in a field I called keycpy,
3. Another field in the global state is initialized to 1; I called this one magicnumber,
4. The actual encryption process consists of: multiplying the magicnumer by itself and multiplying it by the number in the slot of the message (that you previously entered) if the current byte of the key is a one. If the current key byte is a zero then nothing extra happens (see below),
5. Once the encryption is done or stopped by the user, the resulting magicnumber is stored back inside the message slot (overwriting its previous content).

The prettified code looks like this:

while(number_store->size & 8) {
    // do stuff
    std::cout << "Continue Encryption? (y/n)" << std::endl;
    std::cin >> continue_enc;
    if(continue_enc == 'Y' || continue_enc == 'y') {
    number_store->magicnumber *= number_store->magicnumber;
    if(number_store->keycpy[idx] == 1) {
        uint64_t msg = 0;
        read_number_from_store(&number_store->numbers[msg_slot & 0x7F], &msg);
        number_store->magicnumber *= msg;
    }
    } else if(continue_enc == 'n' || continue_enc == 'N') {
    number_store->size &= 0xF7u;
    }
}

As you might have figured, we have basically two avenues (technically three I guess.. but one is clearly useless :-D). Either we load the private key as the message, or we load it as the key parameter.

If we do the former - based on the encryption logic - we end up with no real control over the way the magicnumber is going to be computed. Keep in mind the numbers in the store are all encrypted with the encrypt function and when the key is retrieved out of the store, it isn't decrypted (it is not a normal get operation) but just memcpy'd to the keycpy field like in the below:

memmove(number_store->keycpy, &number_store->numbers[keyslot], 32);

So even if we can insert a known value in the store, we wouldn't really know what it would look like once encrypted.

If we load the private key as the key though, we now have.. an oracle! As the user can stop the decryption process whenever wanted, the attack could work as follows (assuming you would like to leak one byte of the private key):

1. Load the value 3 in the slot 0,
2. Use the private key encryption feature with key slot 18 (where the private key is written at) and message slot 0 (where we loaded the value 3),
3. Depending on the value of the current byte of the key the value of magicnumber could be either be (1*1)*3=3 or (1*1)=1. If the user stops the encryption then this number is written into the store in the slot 0,
4. Get the value in slot 0. If the value is 3 then the key byte was a 1, else it was a 0.

Following this little recipe allows us to leak the bit n, which once done allows you to push the encryption one round further and leak bit n + 1.. and so on and so forth.

This is great, but there are still two small details we need to iron out before carrying the attack properly.

The code that runs before the actual encryption scans the keycpy and skips any leading zeros. This means that if the key were 0b00010101 for example, the actual encryption logic we described above would start after skipping the first three leading zeros. In order to know how many of those exists, we can just trigger the private key encryption feature and encrypt... until you cannot anymore (there are only 32 bytes per number so at most you get 32 rounds). You just have to count how many rounds you went through and the difference to 32 is the number of leading zeros.

The second small detail is that we technically don't know in which slot the private key is stored in on the remote server (remember, the shared library isn't provided to us). Which means we need to find that out somehow. Here is what we know:

1. the key is stored at number_of_rows + 2,
2. the size of the store is initialized to number_of_rows.

If we combine those two facts we can try to read every single slot from the first one until the latest one. First time, it stops with an 'out of range' exception you have your number_of_rows :-)

Oh yeah by the way, remember this third stupid possibility I mentioned earlier? Using the private key as the slot of both the message and the key would basically end-up in.. overwriting the private key itself so not so useful.

Leaking it like it's hot

Here is my ugly python implementation of the attack:

# Axel '0vercl0k' Souchet - 3-March-2018
import sys
import socket

host = ('192.168.1.41', 31337)

def recv_until(c, s):
    buff = ''
    while True:
        b = c.recv(1)
        buff += b
        if s in buff:
            return buff

    return None

def addn(c, r_n, n):
    recv_until(c, '8. Exit\n')
    c.send('0\n%d\n%d\n' % (r_n, n))

def readn(c, r_n):
    recv_until(c, '8. Exit\n')
    c.send('1\n%d\n' % r_n)
    recv_until(c, 'Result is ')
    res = c.recv(1024).splitlines()
    return int(res[0], 10)

def main():
    r_key = 18
    r_oracle = 0
    # first step is to find out how many 0's the key starts with,
    # to do so we ask for an encryption where the key is the pkey,
    # and we encrypt until we cannot and we count the number of
    # 'Continue Encryption?'. 32 - this number should give us the
    # number of 0s
    n_zeros = 32
    c = socket.create_connection(host)
    addn(c, r_oracle, 1337)
    recv_until(c, '8. Exit\n')
    c.send('6\n%d\n%d\n' % (r_oracle, r_key))
    recv_until(c, 'Continue Encryption? (y/n)\n')
    for _ in range(32):
        c.send('y\n')
        n_zeros -= 1
        if 'Continue Encryption? (y/n)' not in c.recv(1024):
            break

    if n_zeros > 0:
        print 'Found', n_zeros, '0s at the start of the key'

    leaked_key = [ 0 ] * n_zeros
    v_oracle = 3
    # now we can go ahead and leak the key bit by bit (each byte is a bit)
    for i in range(32 - n_zeros):
        which_bit = len(leaked_key) + 1
        bit_idx = which_bit - n_zeros
        c = socket.create_connection(host)
        addn(c, r_oracle, v_oracle)
        # private key encryption
        recv_until(c, '8. Exit\n')
        c.send('6\n%d\n%d\n' % (r_oracle, r_key))
        for _ in range(bit_idx):
            recv_until(c, 'Continue Encryption? (y/n)\n')
            c.send('y\n')

        if which_bit < 32:
            recv_until(c, 'Continue Encryption? (y/n)\n')
            c.send('n\n')

        magic_number = 1
        for b in leaked_key[n_zeros :]:
            magic_number &= 0xffffffff
            magic_number *= magic_number
            if b == 1:
                magic_number *= v_oracle

        magic_number *= magic_number
        magic_number &= 0xffffffff
        n = readn(c, r_oracle)
        bit = 0 if magic_number == n else 1
        leaked_key.append(bit)
        c.close()
        print 'Leaked key: %08x\r' % reduce(lambda x, y: (x * 2) + y, leaked_key),

main()

Which should result in something like below:

Conclusion

If you enjoyed this write-up you should also have a look at this post authored by the organizers (there's even source code!): beVX Conference Challenge. A funny twist for me was that the encryption and decryption routines called sleep to simulate a delay that could be timed over the network and used as a side-channel. As every time you have a non-zero byte in the key, the message slot has to get read out of the store which... calls into the decrypt function.

I thought this was pretty fun - even if I were to have played the challenge in time I probably wouldn't have noticed the delay as I would have been working with my own dummy implementations of encrypt and decrypt :-)

Totally unrelated but I also have migrated the blog to pelican as I am basically done using octopress and ruby. I think I did an OK job at making it look not too shitty but if you see something that looks ugly as hell feel free to ping me and I'll try my best to fix it up!

Last but not least, special thanks to my mates mongo and yrp604 for proofreading and edits :)